Ein Auszug aus meinem Buch „IQ – Marathon“
Stellen wir uns ein schachbrettartiges Quadrat mit Zahlen vor, deren Summe in jeder Reihe, jeder Spalte und jeder der beiden Hauptdiagonalen jeweils denselben Wert besitzt. Diese Summe wird als magische Zahl m bezeichnet. Die Forderung, dass Zeilen-, Spalten- und beide Diagonalsummen gleich sind, heißt magische Bedingung.
Insgesamt gibt es 384 pandiagonale magische Quadrate der 4. Ordnung, wo die Zahlen ne-beneinander, untereinander, diagonal und in vier 2×2 Quadraten stets die gleiche Summe bilden. Das gilt auch für das folgende pandiagonale veränderte magische Quadrat mit der magischen Summe 0.
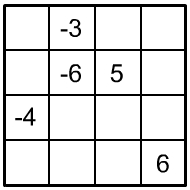
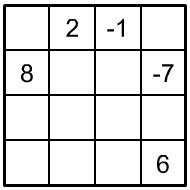
Aufgabe: Verteilen Sie auf diesem Viererquadrat die Zahlen von 1 bis 8 und von –1 bis –8 jeweils nur einmal so, dass die Summe der vierer Zahlen untereinander, nebeneinander, diagonal und der vier 2×2 Eckfelder soll stets die Zahl 0 ergibt.
Beispiel
| Aufgabe | Lösung |
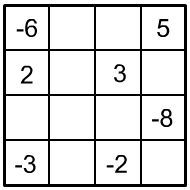 |
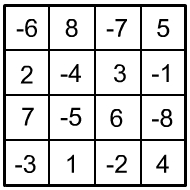 |
Probeaufgaben leicht
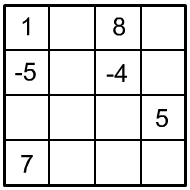
| 1. |
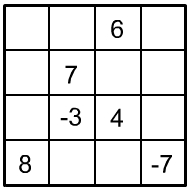
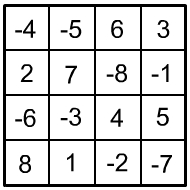
|
2. |
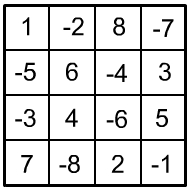
|
3. |
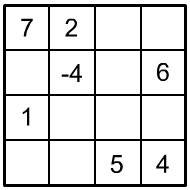
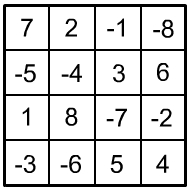
|
| 4. |
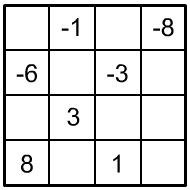
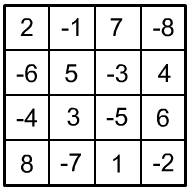
|
5. |


|
6. |
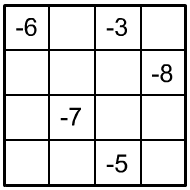
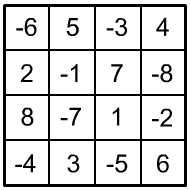
|
Probeaufgaben mittel
| 1. | 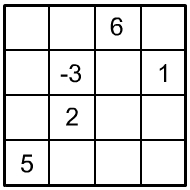
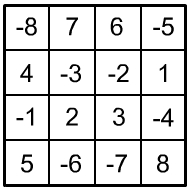
|
2. | 

|
3. | 
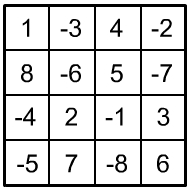
|
| 4. | 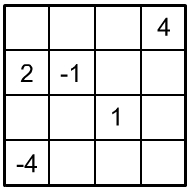
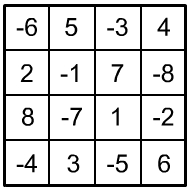
|
5. | 
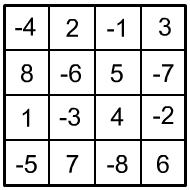
|
6. | 

|
